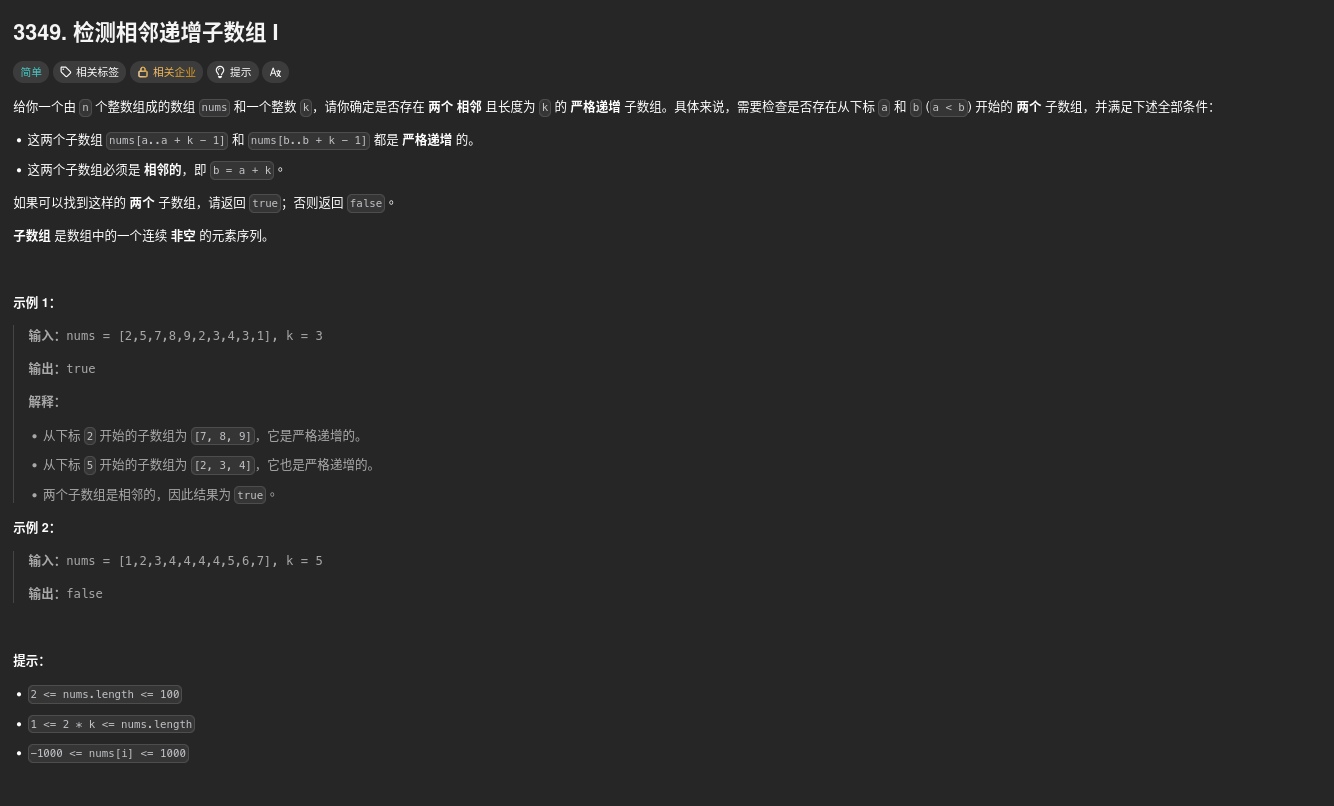
題目:3349. Adjacent Increasing Subarrays Detection I
方法一:暴力枚舉 + 子函式檢查嚴格遞增
- 用一個內部函式 is_increasing(start) 來判斷子陣列是否嚴格遞增。
- 依序枚舉 a,檢查 nums[a:a+k] 與 nums[a+k:a+2k] 是否都嚴格遞增。
- 若找到一組符合條件,立即回傳 True。
- 若都找不到,最後回傳 False。
時間複雜度:
O(n*k),其中 n 是陣列長度,k 是子陣列長度。
class Solution:
def hasIncreasingSubarrays(self, nums: List[int], k: int) -> bool:
n = len(nums)
# 檢查從 index i 開始的長度 k 子陣列是否嚴格遞增
def is_increasing(start: int) -> bool:
for j in range(start + 1, start + k):
if nums[j] <= nums[j - 1]:
return False
return True
# 檢查所有可能的 a (確保 a + 2*k - 1 不超出範圍)
for a in range(n - 2 * k + 1):
b = a + k # 相鄰的下一個子陣列
if is_increasing(a) and is_increasing(b):
return True
return False
class Solution {
public:
bool hasIncreasingSubarrays(vector<int>& nums, int k) {
int n = nums.size();
// 檢查從 start 開始的長度為 k 的子陣列是否嚴格遞增
auto is_increasing = [&](int start) -> bool {
for (int j = start + 1; j < start + k; ++j) {
if (nums[j] <= nums[j - 1])
return false;
}
return true;
};
// 檢查所有可能的起點 a
for (int a = 0; a + 2 * k <= n; ++a) {
int b = a + k; // 相鄰的下一個子陣列
if (is_increasing(a) && is_increasing(b))
return true;
}
return false;
}
};
方法二:利用遞增連續長度(O(n) 解法) (由 ChatGPT 提供)
思路:
我們不需要每次都重新檢查一整段子陣列是否嚴格遞增。
可以一次遍歷整個陣列,記錄「以 nums[i] 結尾的嚴格遞增子序列長度」,
再用這個資訊快速判斷是否存在兩段長度為 k 且相鄰的遞增子陣列。
以 nums = [2,5,7,8,9,2,3,4,3,1], k = 3 為例:
| i | nums[i] | 連續遞增長度 len[i] |
|---|---|---|
| 0 | 2 | 1 |
| 1 | 5 | 2 |
| 2 | 7 | 3 |
| 3 | 8 | 4 |
| 4 | 9 | 5 |
| 5 | 2 | 1 |
| 6 | 3 | 2 |
| 7 | 4 | 3 |
| 8 | 3 | 1 |
| 9 | 1 | 1 |
現在我們知道:
len[2] = 3→ 表示nums[0..2]是遞增(實際上我們關心nums[0..2]是一段長度 3 的遞增子陣列)len[7] = 3→ 表示nums[5..7]是另一段長度 3 的遞增子陣列- 並且它們是相鄰的 (
5 == 2 + 3)
→ 滿足條件
公式推導
當 len[i] >= k 表示有一段嚴格遞增子陣列結束於 i。
那它的起點是 i - k + 1。
我們只要確認「當前這段」的起點是否緊接著前一段遞增子陣列的終點即可。
class Solution:
def hasIncreasingSubarrays(self, nums: List[int], k: int) -> bool:
n = len(nums)
inc = [1] * n
# 計算每個位置的連續嚴格遞增長度
for i in range(1, n):
if nums[i] > nums[i - 1]:
inc[i] = inc[i - 1] + 1
# 檢查是否存在兩個相鄰的長度為 k 的遞增子陣列
for i in range(k - 1, n):
if inc[i] >= k:
start_a = i - k + 1
start_b = start_a + k
if start_b + k - 1 < n and inc[start_b + k - 1] >= k:
return True
return False
class Solution {
public:
bool hasIncreasingSubarrays(vector<int>& nums, int k) {
int n = nums.size();
vector<int> inc(n, 1);
// 計算每個位置的連續嚴格遞增長度
for (int i = 1; i < n; ++i) {
if (nums[i] > nums[i - 1])
inc[i] = inc[i - 1] + 1;
}
// 檢查是否存在兩個相鄰的長度為 k 的遞增子陣列
for (int i = k - 1; i < n; ++i) {
if (inc[i] >= k) {
int start_a = i - k + 1;
int start_b = start_a + k;
if (start_b + k - 1 < n && inc[start_b + k - 1] >= k)
return true;
}
}
return false;
}
};
時間複雜度
- O(n):僅需單次遍歷即可得出遞增長度並檢查條件。
- O(n) 空間:需要一個
inc陣列。
小結
| 方法 | 思路 | 時間複雜度 | 空間複雜度 |
|---|---|---|---|
| 方法一 | 暴力檢查每一對相鄰子陣列 | O(n × k) | O(1) |
| 方法二 | 預處理遞增長度,一次遍歷判斷 | O(n) | O(n) |